阻擋正多邊形
高小組 第二名
縣 市:高雄市
校 名:陽明國小
作 者:蔡政江、羅元琮、侯智文
指導教師:萬國興、陳永富

我是蔡政江我最大的興趣是數學,從小一直很想做科展,在五年級時跟隨萬老師做科展,目前已做了兩年了。數學是我的最愛,從三歲時就開始接觸數學,雖然,學到高中的數學,還是學得零零落落,不是很完整,反而,我覺得科展給我更大的挑戰空間,今後,還要再繼續做科展。
我是羅元琮我不是「柏原崇」,就讀獅湖國小,四年級時,第一次接觸科展,抱著好奇的心理,對數學特別感到有興趣,剛好萬老師開了一個科學小博士的活動,報名了以後就展開了我的科展生活!後來,我就跟著萬老師到處搜集資料,做了三年的科展,每一次總是讓我受益良多,當每次的比賽,看到了別人的作品時,我總是覺自己是多麼的渺小,而提醒我要再加油努力。
我是高雄市陽明國小五年四班的候智文,喜歡做有關數學的問題,我之所以會想要去作科展,是因為我覺得多給自己一個機會去嘗試各種不同的活動,這樣也對自己有所幫助,我的興趣是打籃球、踢足球、打躲避球....。專長是下五子棋、象棋..棋藝之類的東西。我也希望大家跟我一樣喜歡作科展。
一、研究動機
有一次,政江參加香港保良局奧林匹亞第三屆數學競賽比賽前,在高師大進行數學訓練,左教授發給我們一張數學試卷,其中有一題很有趣,內容是說,在一個的正方形棋盤儘可能打最少的「×」,使其找不到四個空格,以空格當頂點,可連成一個正方形:
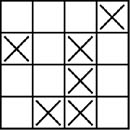
後來,政江和同學討論,我們都覺得這個題目很有挑戰性,我們想;加大棋盤或改變棋盤形狀,是不是能找到規律性?於是在老師的指導下完成下面的研究。
二、研究目的
(一)從簡單的正方形,邊長2×2開始研究,歸納正方形棋盤「×」的個數,得到一般性,再想到正三角形、正六邊形,最後再到長方形。當棋盤的邊加大時,找出「×」記號增加的規律。
(二)從遊戲中來學數學,找尋規律性,寓教於樂,讓我們對數學產生更深的認識,也能引起我們對數學的興趣。
三、問題
(一)正方形的棋盤最少需要多少個「×」記號,才能阻擋小正方形的出現?
(二)正三角形的棋盤最少需要多少個「×」記號,才能阻擋小正三角形的出現?
(三)正六邊形的棋盤最少需要多少個「×」記號,才能阻擋小正六邊形的出現?
(四)長方形的棋盤最少需要多少個「×」記號,才能阻擋小長方形的出現?
(五)正方形的「×」記號的個數,有什麼規律?怎樣安排「×」記號?
(六)正三角形的「×」記號的個數,有什麼規律?怎樣安排「×」記號?
(七)正六邊形的「×」記號的個數,有什麼規律?怎樣安排「×」記號?
(八)長方形的「×」記號的個數,有什麼規律?怎樣安排「×」記號?
四、遊戲規則
(一)正方形棋盤,當「×」記號填完後,裡面不可以再形成一個以空格當頂點的正方形(長方形不在此限)。如下圖的小正方形:
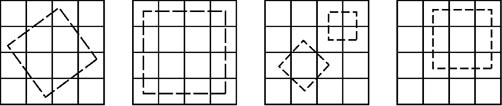
(二)如正三角形的棋盤,儘可能用最少的「×」記號,使正三角形的棋盤內找不到任意以空格當頂點連成一個正三角形。如下圖:
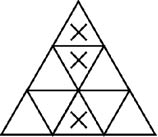
(三)長方形棋盤,因為正方形是長方形的一種,所以也要阻擋正方形。
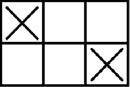
例如:
五、研究過程和方法
(一)正方形(請參閱紀錄)
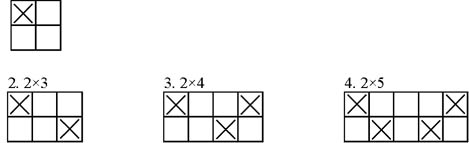
1.2×2(只有1種方式)

2.3×3(共有5種方式)

3.4×4(共有40種方式)
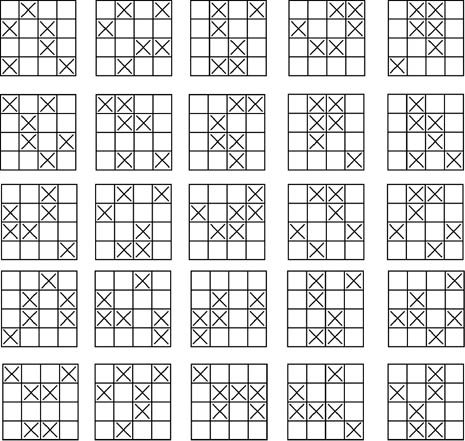
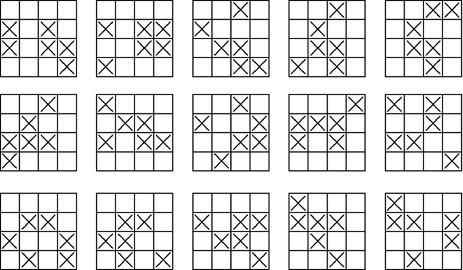
4.5×5(請參閱紀錄)
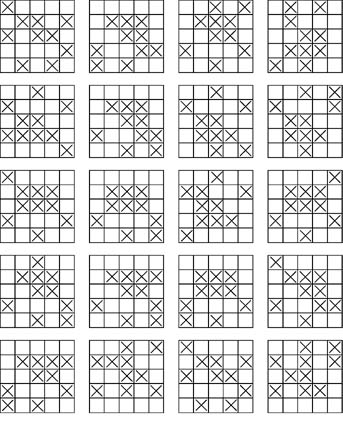
5.我們把「×」的個數整理如下表,卻發現是有規律性。
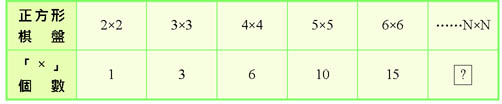
6.既然正方形棋盤是有規律性,讓我們想到正三角形棋盤,是不是也有規律性?因此,我們繼續來完成正三角棋盤。
(二)正三角形(請參閱紀錄)
1.每邊為2 (只有1種方式)
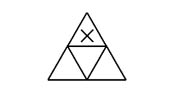
2.每邊為3 (共有2種方式)
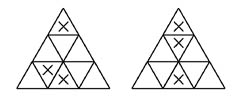
3.每邊為4 (共有2種方式)
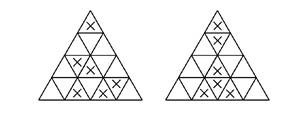
4.每邊為5 (共有2種方式正六邊形)
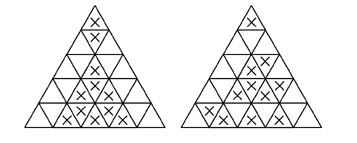
(三)正六邊形
1.每邊為2 (只有一種方式)
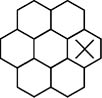
2.每邊為3

3.每邊為4
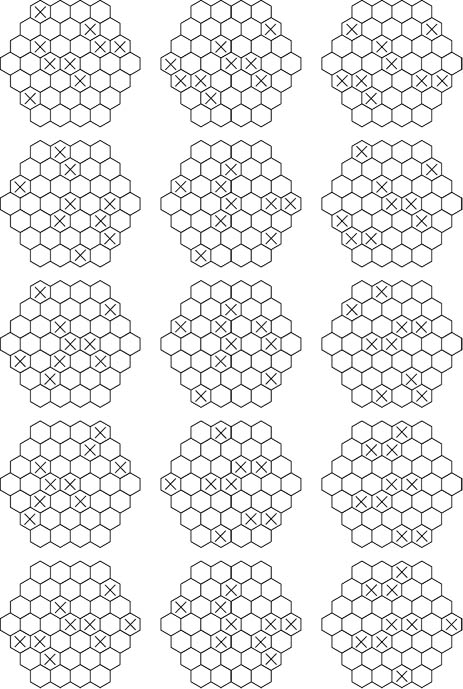
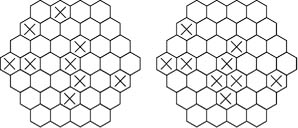
4.每邊為5
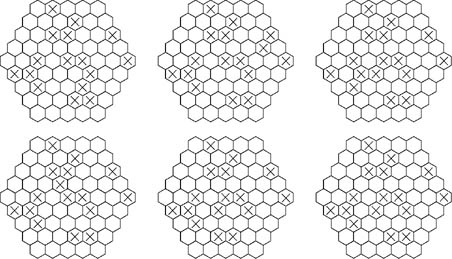
5.正多邊形棋盤做到正六邊形,忽然,我們想到長方形棋盤是不是也有規律呢?
(四)長方形(裡面不可有正方形長方形)請參閱紀錄
1.2×2(最少用四塊組成的長方形、正方形)
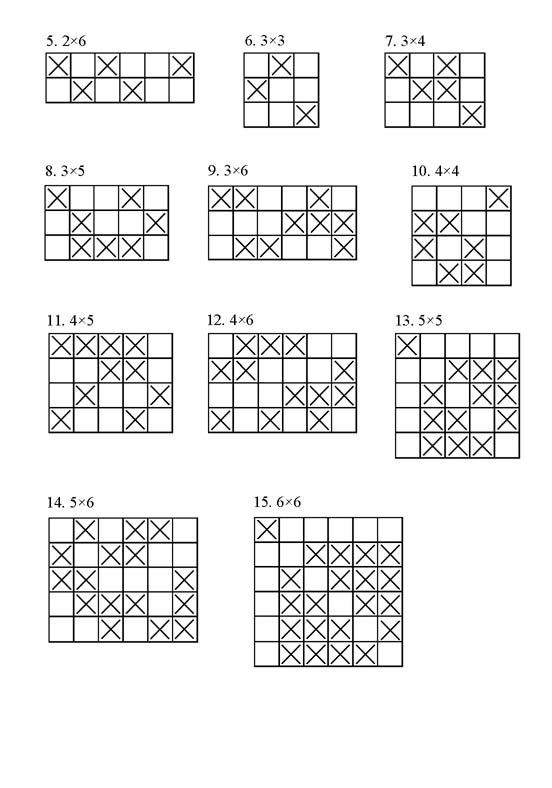
六、討論
(一)正方形安排「×」記號時,本身難度不高,但是無固定的方法,在畫時要注意到許多小正方形。如遊戲規則。
(二)正三角形安排「×」記號,我們發現有二種方法。
1.在三角形畫上兩條虛線,虛線交叉處畫上「×」。
2.在下面四個空格打「×」。
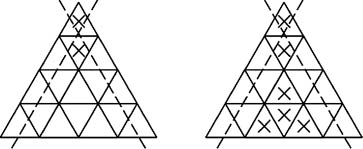
(三)正六邊形,變化多端,更要細心,注意四周圍的小正六邊形,有下列五種類型。
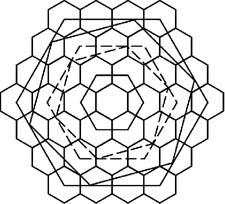
(四)長方形,要注意裡面的小正方形,更加複雜,因畫出的線太多請參閱紀錄。
七、結論
(一)從以上圖形的研究中,發現同類型的圖案所需要的「×」,有異曲同工之妙,隱藏著有趣的規律,經過一番努力後,我們找出了以下的規律:
1.正多邊形:
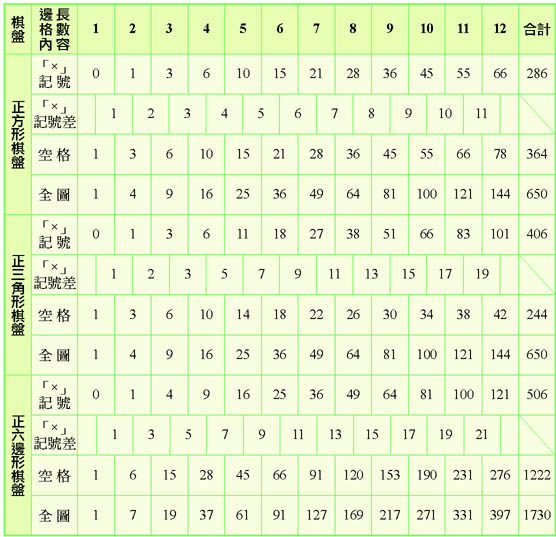
由上表可知:
(1)「×」記號是正三角形最密,正六邊形最疏散。
(2)每一種圖形的「×」記號數都有規律性,所以可以導出公式:
1 設n為邊長,則正方形「×」記號公式為 n×﹙n-1﹚÷2
2 正三角形為 ﹙n-2﹚×﹙n-2﹚+2
3 (r)正六邊形為 ﹙n-1﹚×﹙n-1﹚
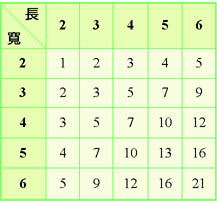
2.長方形,也有規律性,不過要操作一段時間,這個時間隨著長寬加大而變久。例如,假如固定一邊是5的話,要做十幾個棋盤,才能找出規律性。固定一邊是6的話,要二十多個棋盤,才能找出規律性。
(三)因為長方形不是正多邊形,所以雖然有規律性,因為很複雜,涉及很廣,所以無法找到公式。
(四)正三角形在安排「×」記號,是最簡單的,但是找規律性是最困難的。
八、心得與展望
(一)這個實驗讓我們絞盡腦汁,擠破頭殼,尋找「×」記號,不過我們覺得很有挑戰性與趣味性。半年來,我們發揮集體智慧,分工合作,總算找到結果。
(二)未來,我們要朝長方形和正五邊形、正七邊形研究和證明公式的方法,也期望評審先進,給予指教使我們能對數學有深切的認識。
(三)我們發現一種新式的遊戲,利用「阻擋」的策略,探討遊戲輸贏的方法。如附件說明。
九、參考資料
(一)裘宗滬、魏有德、夏興國小學數學資優生輔導教材 九章出版社 1994.8p.530∼630
(二)張遠南使人聰明的智力遊戲 九章出版社 1995.7
(三)張靜嚳、念家興譯數學教學方法 九章出版社 1996
評語
本作品透過數學遊戲討論在一個正方形棋盤中儘可能劃最少的「×」使棋盤中找不到四個空格連成一個正方形,作者從正方形開始再推展到正三角形、正六邊形及長方形;由思考過程中找到規律,作品生動有趣,資料記錄完整是一件優良的作品。