一點破萬線
國中組 第三名
縣 市：台北市
校 名：螢橋國中
作 者：趙家珩
指導教師：項培森
小三開始，在老師鼓勵下，我很喜歡自然學科。國中時，對數學較有興趣，除教科書外，常找生活化的問題研究，覺得數學領域何其寬廣迷人。
參賽過程中，我將平日探討的問題整理、修改，雖需獨挑大樑，但有師長支持，終能順利過關，給我很大信心。
也期望能再挑戰自我、挑戰科展、挑戰極限。
關鍵詞：
等和線、掃描、平移
一、研究動機
曾有同學提出疑問:如何在三角形內找到一個到三邊距離總和為定值的點？嗯…「內心到三邊等距。」「平行線間距離相等。」「交軌法？不對，與『三』邊應該沒有關係。」雖然眾口議論紛紛許久，問題仍然是一團迷霧，這些想法是樣樣有道理，卻個個行不通，使我不禁在課餘時間多看它兩眼。究竟，這問題是否有撥雲見日的一天…？
二、研究目的
探討平面中n條直線間的點到此n條線距離和之變化。
定 義
三、研究設備器材
紙、筆、尺、圓規
四、研究過程與方法
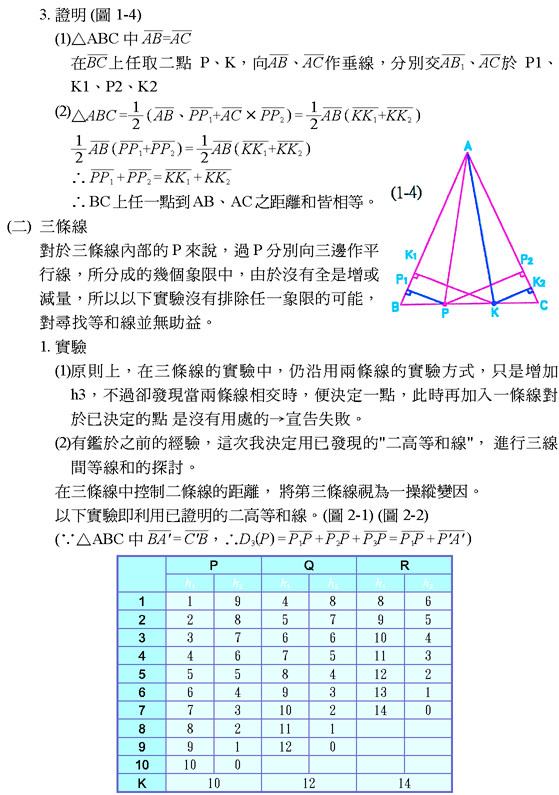
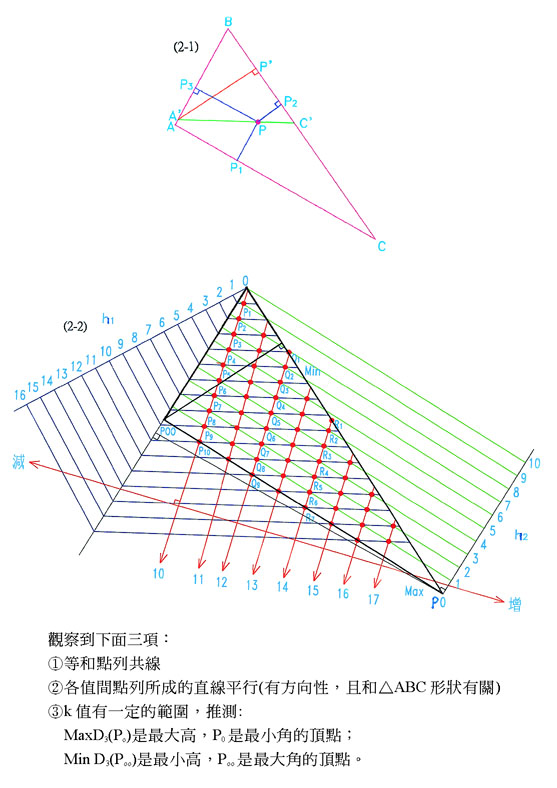
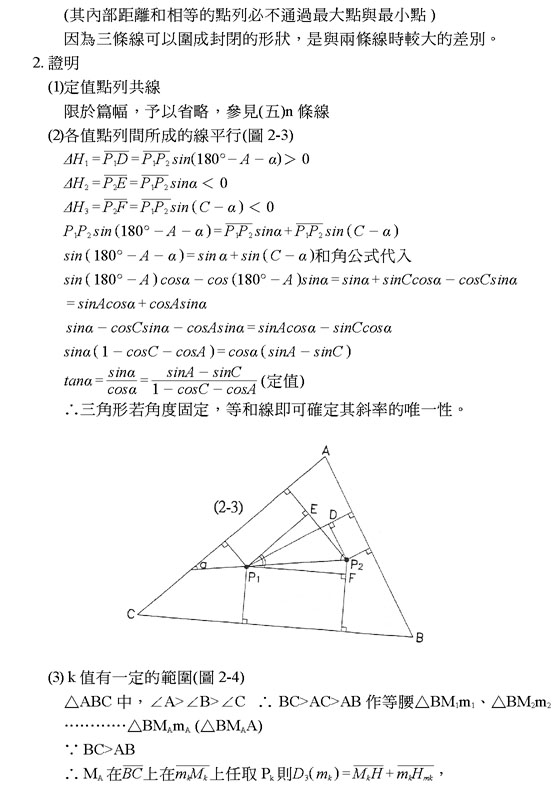
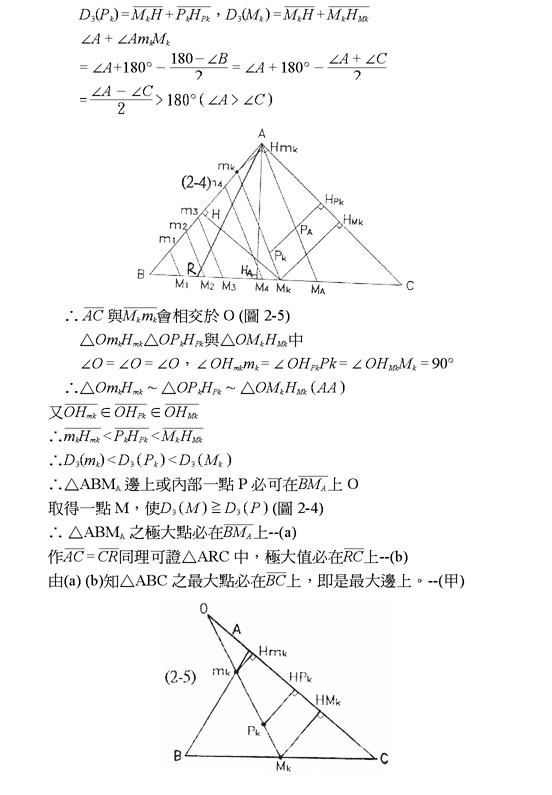
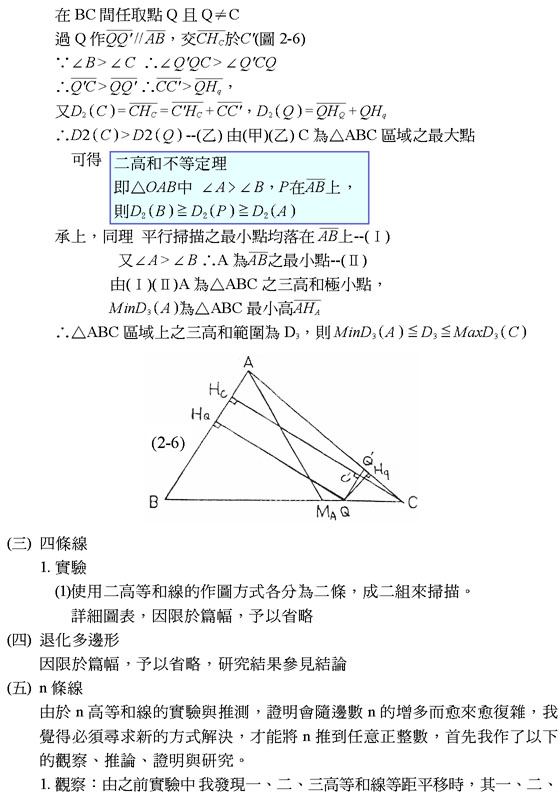
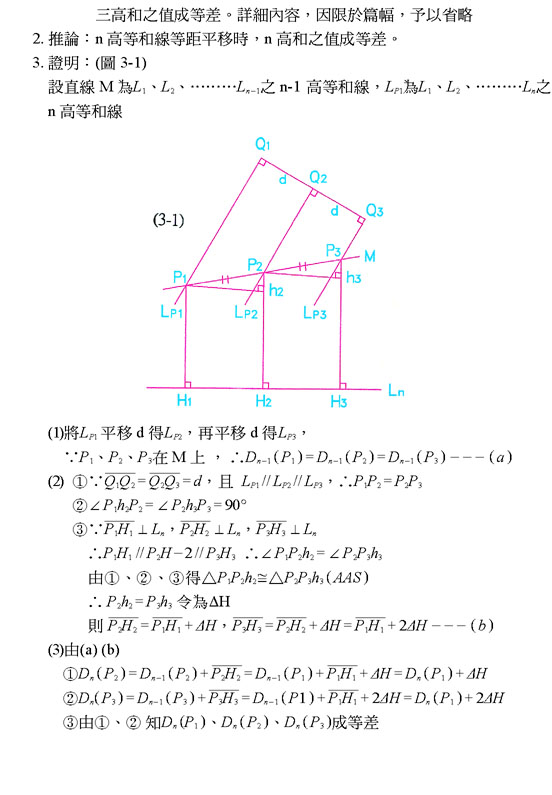
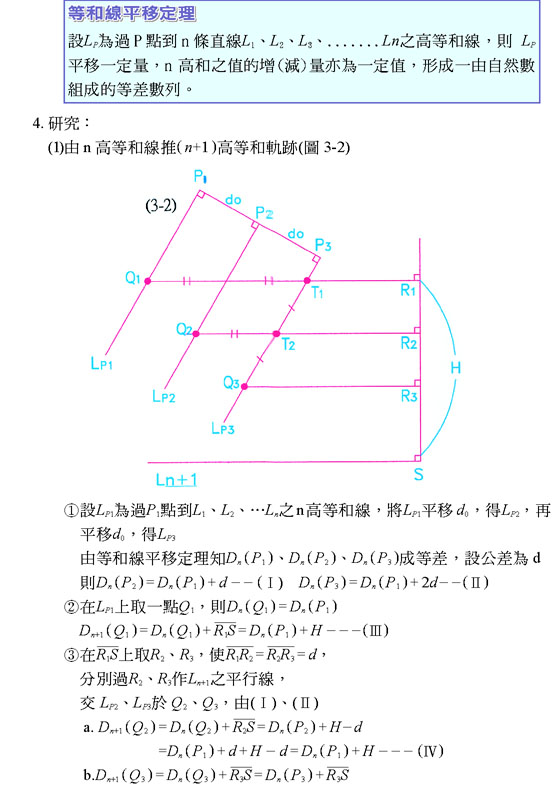
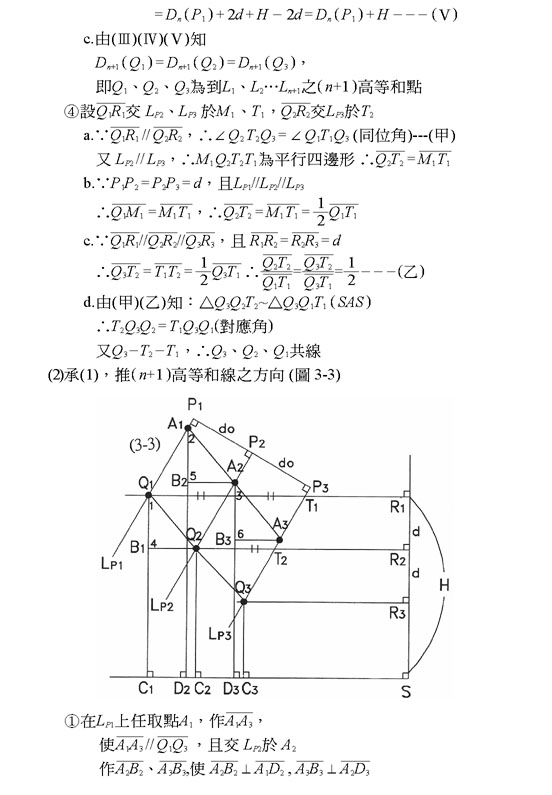
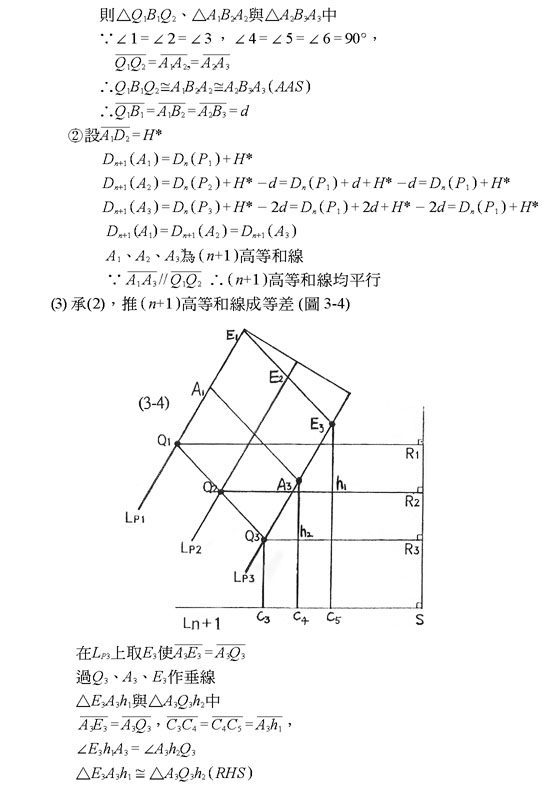
六、 結論
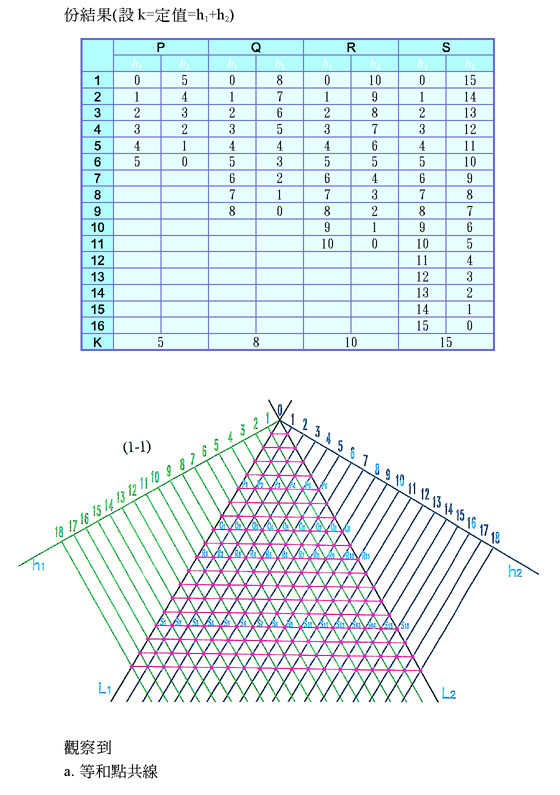
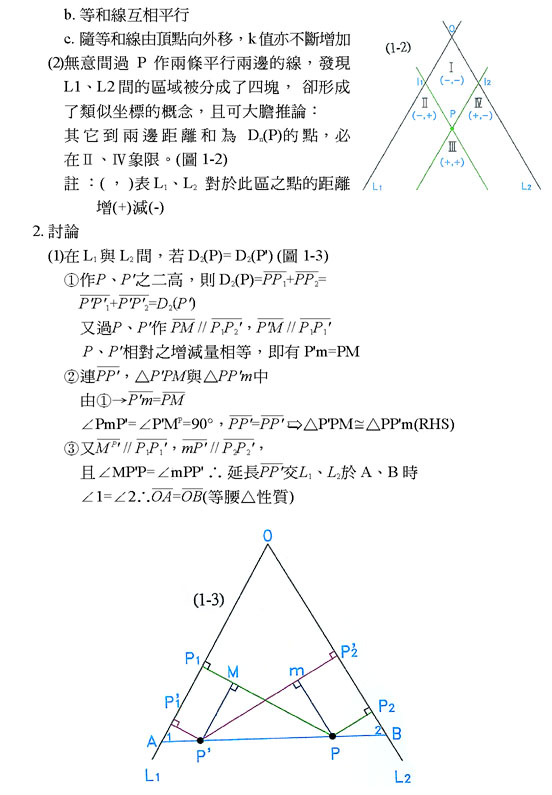
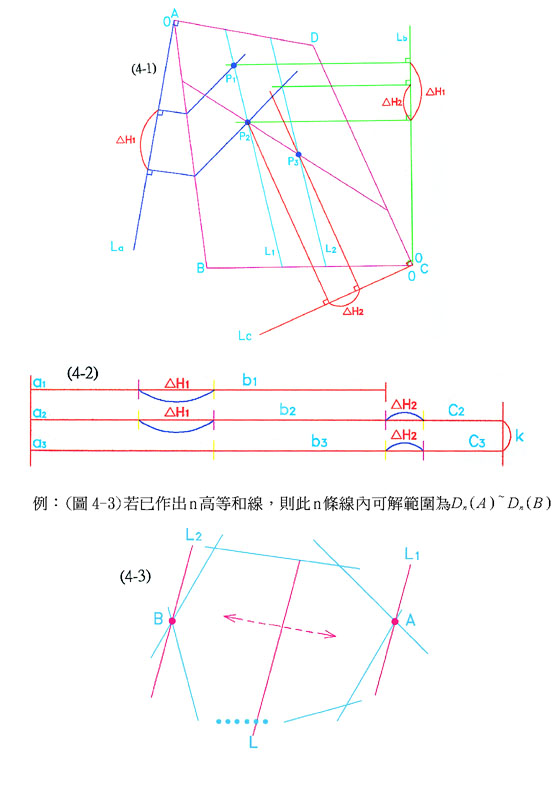
(一)二等高和線L1、L2交於O，在L1、L2 上任取A、B，使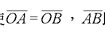
即為此二線的等和線。
(二)n條線內部之等和點會共線，且等和線有一定的方向性及範圍。
(三)巧妙運用有限的平行線及二高等和線，可製作出n邊的等和線。
(四)正△與平行四邊形內部每一點到邊上距離和皆相等;梯形的等和線與二高等和線的意義相同。
七 、參考資料
(一)國中數學第五、六冊
(二)第三十八屆中小學科展優勝作品專輯
(三)高級中學基礎數學第二冊
評語
本作品討論n條直線內部等和點之變化情況，計算細膩，對幾何的知識運用熟練所得之結果對於幾何性質之了解助益即大。