李佳霖，民國七十四年出生於民風純樸的基隆，從小就對各項事物都充滿了濃厚的興趣，特別喜好作數學、看科學類的叢書以及研究物理、化學，「為什麼？」幾乎成了我的口頭禪，真可說是個「好奇寶寶」！

這次有幸承蒙老師的細心指導，能夠有機會參加全國科展，和各地的高手一較高下，使我了解到學問是無止境的，這世界上還有許多奧妙的事物等著我去發掘呢！對我而言，這將是一個畢生難忘的經驗。

一、研究動機

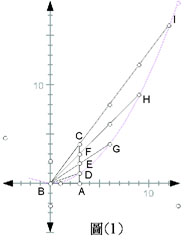
在一本課外讀物中有一道題目談到：在直角三角形中，若將一邊四等分，沿著等分點，作一倍、二倍、三倍、四倍的投射，則四投射點在同一拋物線上，如圖 。我對此種投射法感到非常有趣，於是開始了相關的研究。

二、研究目的

分別以三頂點為投射源點時，作1/N倍投射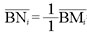，的圖形，及N倍投射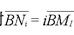的圖形。

探討將「特殊點」作為投射源點時，圖形的變化與性質。

利用此投射系統投出其它的圓錐曲線－橢圓、雙曲線。

三、研究過程

PART A：相異投射源

在向外延伸的部份前，先探討向內縮的部份，如圖 ，將三角形一邊二等分，延等分點，作1倍、1/2倍、1/3倍的投射，則三投射點在一直線上，此性質是否可推廣下去？

性質二

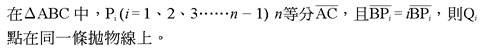
接下來將投射點擴充至三角形三頂點，結果發現當三角形的三邊被n等分時，各邊第一個等分點與頂點相連的線段交點中所形成的三角形必會與原三角形相似，其邊長也可由下表導出：如圖

性質三

任意三角形各邊被n等分時，其第一等分點與對面對應頂點的三交點所形成的三角形必與原三角形相似且邊長比為(2n-1)：(n-2)

由圖 中各頂點與各邊等分點外延皆可形成拋物線，共六條拋物線，接下來開始探討拋物線所形成的交點構成的三角形與原三角形是否也有相似的關係？首先計算這六條拋物線的方程式，發現六條拋物線的對稱軸皆平行原三角形的投射邊。

性質四

任意一個三角形邊長的N等分點投射後所造成的拋物線，其對稱軸必平行原三角形的對應邊。

六條拋物線的交點中，共可形成五個與原三角形相似的三角形。

性質五

六條拋物線交點所形成的三角形均與原三角形相似，且原三角形與其邊長比分別為

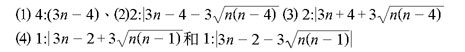
再探討諸相似三角形對應頂點的關係，發現對應點皆在原三角形的中線上。

性質六

向內縮1/N倍及內外延伸N倍所形成的三角形，其頂點皆會在原三角形的中線上，故可知這些三角形都是由「重心」向原三角形的頂點投射出去的相似三角形。

Part B 相同投射源

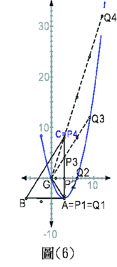將投射方向擴充至各邊，也都會形成拋物線，且六條拋物線均經過投射源點。

同樣地，計算六條拋物線的交點，發現和在PART A一樣，拋物線的交點形成的三角形亦與原三角形相似。

性質七

六條拋物線亦可形成與原三角形相似的三角形，邊長比分別為 4：(n+2)、1：(n+1)，且各相似三角形對應點亦在原三角形的中線上：

Part C 其他的圓錐曲線

在座標平面上，由原點往AC 投射，由前文的探討，得知：

當向外作有規律的N倍，投射時，造成的P點軌跡為拋物線

當向內作有規律的1/N倍，投射時，P點軌跡為一直線。

除了這兩類圖形外還有其他種類的圖形嗎？

為了進一步的研究這現象，在此採用極座標觀念探討，因為極座標的觀念本身就很像此N倍投射，若使用它可能更容易看出投射軌跡方程式的玄機。

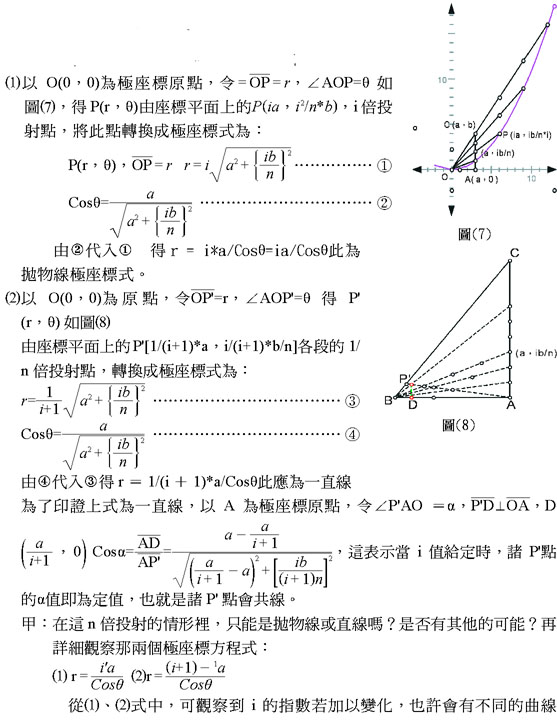
　　此可看出當n、a、b指定後，由t= -1/2僅可畫出一個雙曲線，但可藉由K值的改變而得到無限多的拋物線

乙：更進一步的要去探討的是，在這種n倍投射的環境中，是否有機會造成橢圓呢？那種橢圓又位於何處？

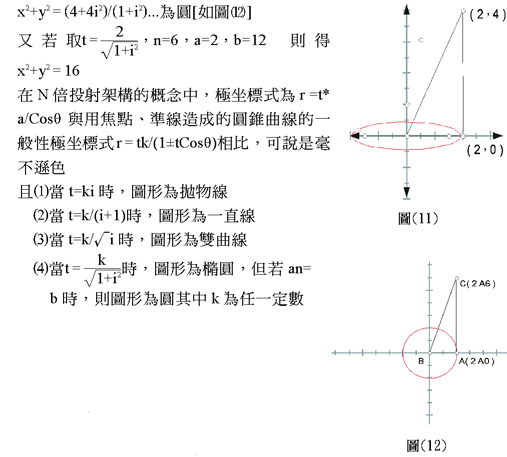
四、結論

1.以三角形的一頂點為投射源點，對邊n等分點為方向，若依投射，則成拋物線排列，依       投射，則成直線排列。

2.分別以三角形的三頂點為投射源點及三角形的重心為投射點，向各對邊n等分點為方向同時投射出拋物線，則拋物線交點所形成的三角形皆與原三角形相似。

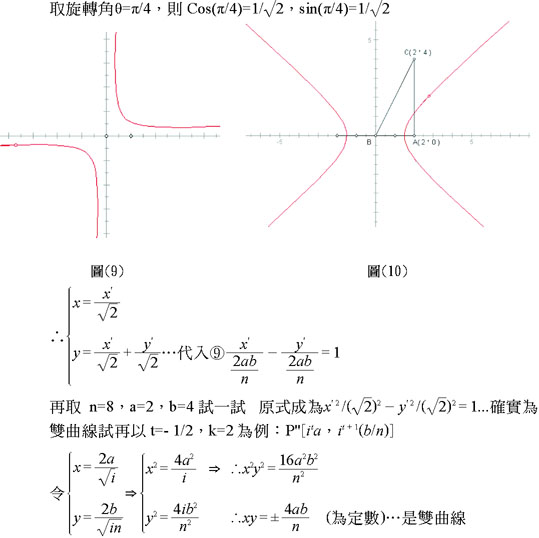
3.擴展 i 倍投射及1/i 倍投射成為it倍投射，其中t= -1/2、-1/4、-1/6...時，圖形成為雙曲線。

4.擴展為倍投射時，圖形成為橢圓，使an=b時，圖形成為圓。

五、參考資料

1.大陸地區數學競賽題解(1995)

2.胡炳生、胡禮祥著   九章出版社

評語