空間中的剛體運動
高中組 第一名
縣 市：台北市
校 名：北一女中
作 者：李佳霖
指導教師：戴青田
翁錫伍
李佳霖，民國七十一年出生於台北，曾畢業於國立北師附小，北市大安國中，現就讀於北一女中二年級。我是個樂觀開朗並愛好運動的女孩，從小就對數學及電腦充滿興趣。感謝良好的小學教育環境，讓我培養了好奇與勇於表達的能力；國中時在父母不讓我補習的原則下，磨練出我的學習與思考力，並養成組織問題深入探討的習慣。上了高中，我加入資訊研習社並有幸在去年的國際科展獲得香港正代表與今年在全國展的成績，實在要感謝戴青田及翁錫伍老師的指導，還有支持我的師長及同學們。科展帶給我的成長實在太多了，我將珍惜這難得的經驗，繼續努力下去！
關鍵詞：剛體運動、立體模擬
一、研究動機
由於螢幕保護程式產生的有趣立體圖形動畫，引發我的興趣想進一步探討是否可以以數學為工具處理大量的圖形運算取代卡通式的貼圖進而探討剛體的運動及其３Ｄ動態式模擬。
二、研究目的
(一)以２Ｄ電腦螢幕呈現剛性物體在空間中做任意運動及受限運動之模擬。
(二)剛體在做各種不同條件之剛性運動時，其視覺軌跡與運動現象之探討。
(三)非透明剛體運動時之遮蔽問題。
三、研究設備器材
586個人電腦、QBasic、Visual Basic(程式設計軟體)、GSP(動態幾何畫板)
四、研究過程方法
第一章、 剛體的自由運動
探討1.1
定點平移(略)
探討1.2
定向平移（略）
探討 2
定軸旋轉
求空間中一點對任意軸之旋轉座標參數
一質點
對空間中任一過點
的直線L旋轉角，其座標參數為
。設此點對L的正射影點為
，過
以L方向向量為法線向量的平面E為旋轉面，求旋轉時座標參數：
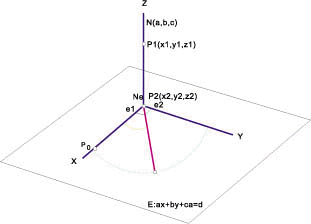
方 法 一
綜合性質求法(略)
方 法 二
建立旋轉正交基底法
(1)求 
代入上式得 
(2)求 
(3)求 
單位向量 
(4)求 
單位向量 
(5)求 
(6)
則
模擬1
萬象旋轉加平移運動
說明：欲模擬一立方體在空間中依給定之方向及旋轉自由平移旋轉。
模擬建立之流程
|
１•輸入 (1)立方體各點座標： (2)平移向量：水平方向角汐，鉛垂方向角汕 (3)旋轉軸向量：水平方向汐，鉛垂方向角汕，旋轉軸上一點
|
|
２•3D運動座標程式運算 (1)求旋轉座標參數： 於旋轉面建立正交基底得兩垂直向量 旋轉座標參數： (2)求平移座標參數： (3)求平移旋轉合成參數 算得各頂點在旋轉
|
|
|
|
模擬2.1
似行星公自轉運動之軌跡探討
設質點O2(R1,0) 繞O1(0,0) 作等角速
之圓周運動，另一質點
繞O2作等角速
之圓周運動，則ｔ時刻P2運動至P2t則
(1)P2t座標參數為：
(2)P2t至O1之距離參數為：
(3)
與
之關係與P2t之軌跡形狀：(推導過程略)
1.當
點軌跡為以往(0,0)為圓心
長為半徑之圓
2.當
，軌跡為橢圓，中心為原點
，長軸長
，短軸長
長軸與X正向夾
角
3.當
，軌跡為 
葉內擺線，有 
個離心最遠點出現在 
時有 
個離心最近點出現在 
時， 
。
4.當
，軌跡為
葉包心線，有
個離心最遠點出現在
時，有
個離心最遠點出現在
時，
軌跡週期
5.當
，軌跡為
葉星壯線，有
個離心最遠點出現在
時，有
個離心最遠點出現在
時，
軌跡週期
模擬2.2
共面衛星軌道模擬（略）
第二章 具阻礙面的設限運動
模擬剛體在受條件限制阻礙的空間中運動的情形。將此類運動型態分為
(一)貼面滑動之多元模擬－正交基底法的推廣運用（略）
(二)貼面滾動之運動模擬
欲模擬空間中一剛體沿一接觸面滾動的情形。
探討１
模擬1
方體對平面滾動
(1)因條件的限制使得方體在滾動時可找到一和平面Ｅ垂直的投影面，可以在此投影面上建立二維座標系，討論此投影圖形各點的座標參數，再以正交基底用線性組合將二維座標轉換成空間中的立體座標。
(2)討論２Ｄ投影座標：
將軌跡對象擴展到正多邊形(即正N角柱對平面滾動)求出通式：
1.其中一頂點Ａ之各分段點座標Ai：
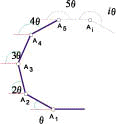
2.各分段旋轉運動函數
為
對
旋轉
角至
的運動座標
(3)將２Ｄ座標轉回３Ｄ座標，建立3D空間中正N角柱在平面上的滾動模擬
模擬2
方體沿球面滾動
(1)對投影面建立正交基底
(2)對投影面建立２維座標系統並討論各投影點的座標參數：
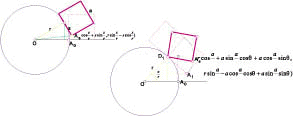
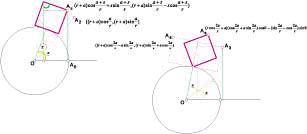
模擬3
球體對平面滾動（略）
模擬4
球體對球面滾動（略）
(三)具兩阻礙面之受限運動
有界扭擺運動模式探討（剛體兩質點在特定軸上運動求其他質點運動的視覺軌跡）
定理1
交於
點，
分別為
上動點，
為定值，令
為
上一點，
，則
軌跡為中心為
點之橢圓：
定理2
夾角
交於
分別為其上兩動點，
為定值。
為
上一點，且
；
為
外一點，且
為定值，則
點軌跡均為一中心為
點之橢圓。
定理3
第三質點軌跡長短軸定理
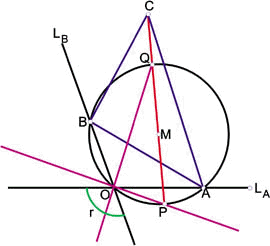
夾角
交於
分別為其上兩動點，
為定值，
為
上一點， 且
為定值依定理6.3中作
交圓於
則
點的橢圓軌跡滿足在
上的軸半長為
，在
上的軸半長為
定理4
放射線共軸定理
呈上定理,若不同的第三質點位於以M為放射中心，向圓外放射的同一射線上，則各質點橢圓軌跡共長軸。
定理5
圓形波等跡定理
呈前定理,若以Ｍ為圓心,作同心圓系向外擴散,則同一圓上的和放射線交點所產生的軌跡全等；並可於同心圓系中找到一和其上質點具相似之軌跡的圓（橢圓長短軸比值相等）
定理6
軌跡旋轉定理
呈前定理，若Ａ繞Ｍ旋轉
角得Ｂ點則Ａ點軌跡以Ｏ為中心旋轉
角得Ｂ點軌跡。
(四)
具多阻礙面的受限運動
空間中的碰撞運動模擬
若有一小球
沿
前進至平面Ｅ，在
處發生反彈，求反射線的方向向量？
(1) ∵
在平面E上
以下令
(2)令Ｍ為過法向量線上的投影且Ｍ(x',y',z')
(3)
在法線上之對稱點為 
則：
(4)反射線方向向量為 
則：
由以上討論為基礎在設計偵測程式從啟動位置與入射向量來推算反射面方程式執行反射後再將反射線改為新入射線，重新執行即可模擬３Ｄ之立體反射。
第三章 ３Ｄ模擬系統的建立
(一)基礎透視投影座標系
以距離觀察者d處，垂直主視線的平面為２Ｄ模擬平面ｘｙ平面，主視線向量為ｚ軸正向建立空間座標系統，並令觀察者的高度為ｈ則：
(二)即時模擬系統的建立
1.令視點
視線向量為
在
上取 
使
以
為原點建立２Ｄ投影面Ｆ使Ｆ垂直
：
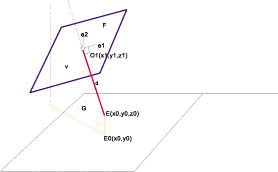
(1)F之方程式：
(2)在F上建立正交基底
令空間中一點
在ｆ平面上的投影為
則有：
∵在Q上F則
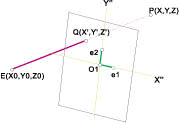
2.令
則有：
3.P在Ｆ上之投影絕對座標為：
4.進行３Ｄ和２Ｄ座標轉換
設 
Q在F上之2D模擬座標為(a,b)
以上述方程式可得P之即時模擬座標，可執行動態模擬視線之即時模擬。
(1)球面模擬系統的建立
1在距Epd處建立球面B(EP,R)表示以Ep為球心半徑Ｒ的球面：
令空間中一點P(X,Y,Z)在B(EP,R)上的投影點為Q(x',y',z')
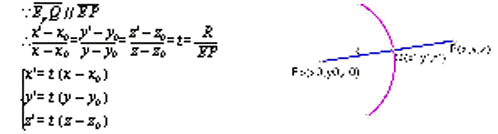
2假設有一球面銀幕B(EP,R)如下圖Ｌ為水平基準軸向右為＋，直線Ｍ為鉛垂基準軸向上為＋，令Ｑ點為以EP為中心，Ｒ為半徑由Ｌ水平旋轉 
角 ，在沿鉛垂面上旋 
角後之對應點：
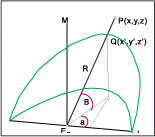
可由球面螢幕模擬視角達1800之廣角模擬且０視差（即物體不變形）
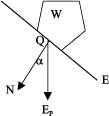
(2)凸體遮蔽現象探討
令觀察者由視點
見一凸形體W上一點Q。過Q作W之切平面E，令E之法線向量為
與
夾
角，則：
五、研究結論
在第一章剛體的自由運動中，本研究以向量求得質點的平移座標參數，並以在旋轉面建立正交基底的方法取得質點在空間中旋轉的絕對座標參數式，以進行由多質點所組成的剛體自由運動模擬。(可自由控制模擬對象的平移方向及旋轉軸角度方位)在此章運動軌跡探討方面，本研究針對剛體做公自轉的運動模擬討論其公自轉速度比與所形成軌跡（為內外擺線）之關係（請參見p.9公自轉軌跡探討結論）於第二章具阻礙面的設限運動中，以在３Ｄ空間建立平面正交基底方法處理剛體在空間中一平面上運動的模擬﹔而貼面運動的滾動模擬則討論以正ｎ面體對平面滾動，正立方體對球面滾動，球體對平面滾動，球體對球面滾動的模擬。求得模擬對象上一定點在運動時的分段座標參數，以一般式表示，並探討同時刻各頂點分段軌跡關係。
而有界扭擺運動是具兩受限面的設限運動，本研究以幾何證明平面上當剛體有兩點固定在兩相交軸上運動，其剛體上之第三質點所成軌跡為橢圓，且完整描述不同第三質點所產生之橢圓軌跡關係。碰撞運動模擬是具多受限面的設限運動，利用向量計算空間中的模擬對象在碰撞到受限面後的立體反射向量。
第三章是３Ｄ模擬系統的探討，本研究共提出三種系統。一為透視公式的座標轉換（視點固定），一為即時更新視點模擬系統，透過此系統可達成觀察者與運動物體相對關係改變（移動或變換視角）的視覺模擬。而後再提出球面模擬螢幕無退縮變形現象的構想。最後是非透明體遮蔽現象的探討，利用剛體面的法線向量與觀察者視線向量的關係決定剛體面運動時可見與否。
本研究所有模擬動畫圖形其座標方位均是由數學計算推導而成，故可任意調整運動條件，此為卡通式貼圖動畫所不能者。
評語
作者討論如何模仿空間簡單圖形沿著某一空間曲線滾動，並將之投影到視覺平面，並以電腦螢幕呈現之。其討論方法，考慮的問題，使用的技巧，呈現多樣而深入的數學內容，頗有數學眼光。比起作者去年的作品進步幅度極大。
回到目錄頁../Index.htm
(請參照探討2)
(
為質點到旋轉軸之正射影長）
(請參照探討1)
角及平移
單位時瞬間之空間座標